Binary Decision Diagram (BDD)
We want to have a representation of circuits that is:
- Compact
- Efficient to manipulate
- Easy to compare
Boolean Functions
A Boolean function is a function $f:$ {0,1}$^k \rightarrow$ {0,1}
Note that Boolean functions are different from Boolean expressions. A Boolean function can be expressed as different Boolean expressions that are logically equivalent. Take the circuit for XOR as an example: $F(A,B) = (A + B)\cdot(\overline{A\cdot B}) = A\cdot\overline{B} + \overline{A}\cdot B$
| A | B | F |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Binary Decision Trees
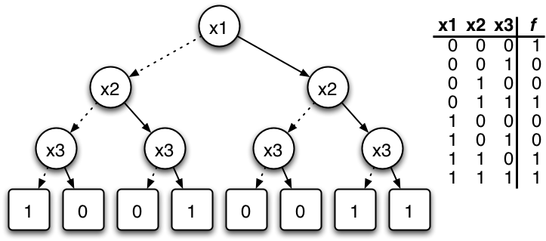$f(x1,x2,x3) = \bar{x_1}\bar{x_2}\bar{x_3}+x_1x_2+x_2x_3$
The size is exponential in the size of number of variables, so it is not a compact representation.
- Each nonterminal vertex v is labeled by a variable var(v) and has arcs directed toward two children:
- lo(v) (shown as a dashedline) corresponding to the case where the variable is assigned 0, and
- hi(v) (shown as a solid line) corresponding to the case where the variable is assigned 1.
- Each terminal vertex is labeled 0 or 1.
Shannon Decomposition
$f = x \cdot f_x + \bar{x} \cdot f_{\bar{x}}$
$f_x$ and $f_y$ are the resulting functions when some argument $x$ is assigned a constant value of either 0 or 1. They are called cofactors of $f$.
We can use this formula to turn a boolean function into a BDD.
ROBDD
Reduced, Ordered, Binary Decision Diagram (ROBDD), usually referred to as just BDD, discussed by Bryant (1992) in the paper Symbolic Boolean manipulation with ordered binary-decision diagrams, is an efficient data structure for representing and manipulating Boolean functions symbolically. It gives a canonical representation of a boolean function as a directed acyclic graph (DAG). Canonicity means if the order of the variables are fixed, then each boolean function has a unique representation as an ROBDD. This means we can compare boolean functions by constructing their ROBDDs and checking if they are equal by a simple pointer comparison. The technique is useful for equivalence checking two circuits (e.g. original circuit and an optimized one).
Reduction of Decision Tree to BDD
-
Remove Duplicate Terminals
Eliminate all but one terminal vertex with a given label and redirect all arcs into the eliminated vertices to the remaining one.
-
Remove Duplicate Nonterminals
If nonterminal vertices u and v have var(u) = var(v), lo(u) = lo(v), and hi(u) = hi(v), then eliminate one of the two vertices and redirect all incoming arcs to the other vertex.
-
Remove Redundant Tests
If nonterminal vertex v has lo(v) = hi(v), then eliminate v and redirectall incoming arcs to lo(v)
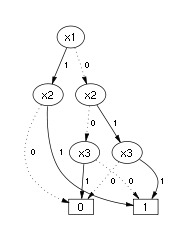The BDD we get after applying the reductions for $f$.
Applications
digital system design, verification (SAT solving), and testing
Encoding Sets
Encoding Relations
CUDD
CUDD is a C++ package to manipulate BDDs.