The Sieve of Erathothenes
The Sieve of Eratosthenes is an algorithm used to generate prime numbers. Given a limit of some positive integer n, the algorithm will output all prime numbers up to the limit.
It takes advantage of the Fundamental theorem of arithmetic, which states that every integer greater than 1 either is prime itself or is the unique product of prime numbers.
Starting with the smallest prime number 2, the algorithm crosses off its multiples, and it then get the next number not crossed off, 3, which is also a prime number, and cross off its multiples. Repeat this process on and on until we hit square root of n.
The animation on wikipedia illustrates this process nicely:
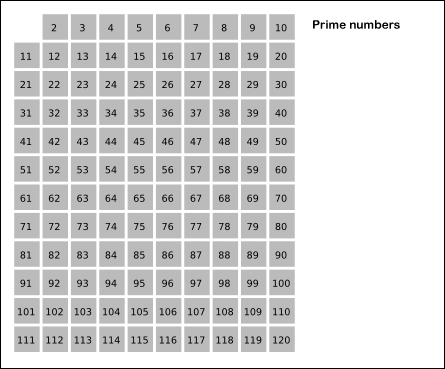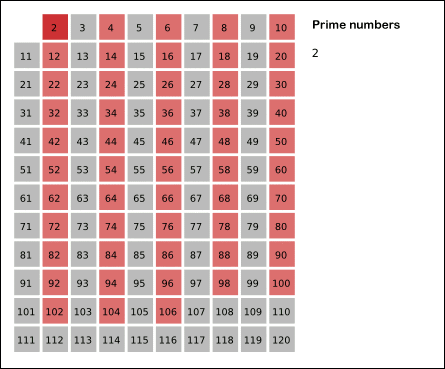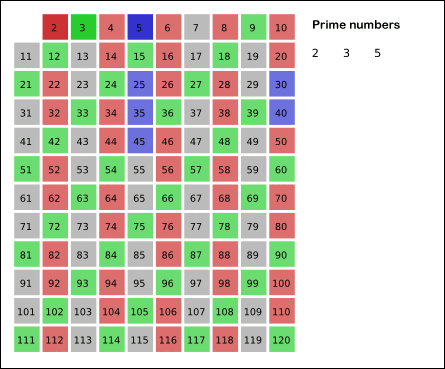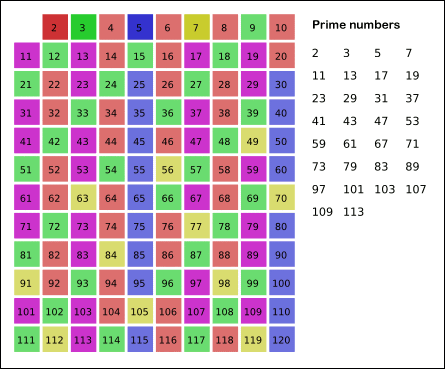
A Python implementation of the algorithm:
import math
"""
Sieve of Eratothenes
"""
def sieve(n):
"""yield prime numbers up to n"""
if n < 2:
return []
else:
is_prime = [True] * n
is_prime[0] = is_prime[1] = False
for i in range(2, n):
if is_prime[i]:
yield i
for num in range(i*i, n, i):
is_prime[num] = False
def sieve_verbose(n):
"""Generate a list of prime numbers up to n"""
if n < 2:
return []
else:
is_prime = [True] * n
is_prime[0] = is_prime[1] = False
for i in range(2, math.floor(math.sqrt(n))):
if is_prime[i]:
print("{} is prime".format(i))
print("Removing multiples of {}:".format(i))
removed = []
for num in range(i*i, n, i):
is_prime[num] = False
removed.append(num)
print(removed)
primes = []
for i in range(2, len(is_prime)):
if is_prime[i]:
primes.append(i)
return primes
size = 120
primes = sieve_verbose(size)
print("Prime numbers up to {}:".format(size))
print(primes)Output:
2 is prime
Removing multiples of 2:
[4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40, 42, 44, 46, 48, 50, 52, 54, 56, 58, 60, 62, 64, 66, 68, 70, 72, 74, 76, 78, 80, 82, 84, 86, 88, 90, 92, 94, 96, 98, 100, 102, 104, 106, 108, 110, 112, 114, 116, 118]
3 is prime
Removing multiples of 3:
[9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48, 51, 54, 57, 60, 63, 66, 69, 72, 75, 78, 81, 84, 87, 90, 93, 96, 99, 102, 105, 108, 111, 114, 117]
5 is prime
Removing multiples of 5:
[25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90, 95, 100, 105, 110, 115]
7 is prime
Removing multiples of 7:
[49, 56, 63, 70, 77, 84, 91, 98, 105, 112, 119]
Prime numbers up to 120:
[2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113]