Linear Regression in R
Implementing Linear Regression
Using the closed form formula for beta minimizing the mean squared error (MSE):
$\hat{\beta} = (X^TX)^{-1}X^TY$
linear <- function(y, X) {
# fit a linear model
beta <- solve(t(X) %*% X) %*% t(X) %*% y
return(beta)
}
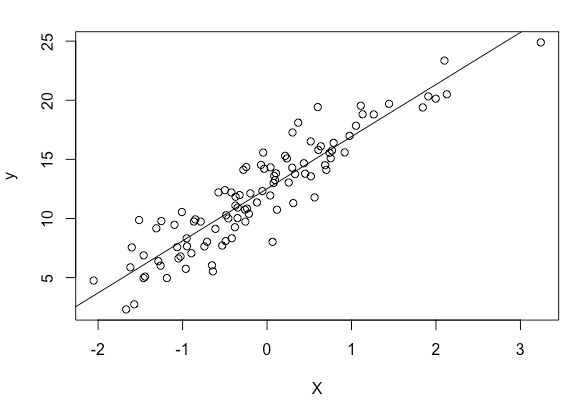
# simulate some data:
n <- 100
X <- rnorm(n)
# the "true" function plus Gaussian error:
y <- 4.5*X + 12.345 + rnorm(n, 0, 1) * 2
plot(X, y)
# augment X with a column of 1's
X <- cbind(X, rep(1,n))
# fit the model
beta = linear(y, X)
# plot the fit line
X <- -10:10
y <- beta[1] * X + beta[2]
lines(X, y)
Using lm For Fitting Linear Models
lm is used to fit linear models. Type ?lm in RStudio for help and documentation.
For the above example, model <- lm(y ~ X) will fit a linear model to the data.
Another example: prostate cancer dataset. The description of the dataset can be found here.
> dat <- read.table('prostate.data')
> head(dat)
lcavol lweight age lbph svi lcp gleason pgg45 lpsa train
1 -0.5798185 2.769459 50 -1.386294 0 -1.386294 6 0 -0.4307829 TRUE
2 -0.9942523 3.319626 58 -1.386294 0 -1.386294 6 0 -0.1625189 TRUE
3 -0.5108256 2.691243 74 -1.386294 0 -1.386294 7 20 -0.1625189 TRUE
4 -1.2039728 3.282789 58 -1.386294 0 -1.386294 6 0 -0.1625189 TRUE
5 0.7514161 3.432373 62 -1.386294 0 -1.386294 6 0 0.3715636 TRUE
6 -1.0498221 3.228826 50 -1.386294 0 -1.386294 6 0 0.7654678 TRUE
# split into training and test set
x <- sample(rep(1:8,each=12))
dat.tr <- dat[x != 1,]
dat.te <- dat[x == 1,]
# fit a full model with all features
full <- lm(lpsa ~ ., data=dat.tr)
# training error
tr_err.full <- predict(full)
with(dat.tr, mean((lpsa - tr_err.full) ^2))
# test error
pr.full <- predict(full, newdata=dat.te)
with(dat.te, mean((lpsa - pr.full) ^2))
# fit a reduced model with a subset of features
reduced <- lm(lpsa ~ lcavol + svi + lcp, data=dat.tr)
# training error
tr_err.reduced <- predict(reduced)
with(dat.tr, mean((lpsa - tr_err.reduced) ^2))
# test error
pr.reduced <- predict(reduced, newdata=dat.te)
with(dat.te, mean((lpsa - pr.reduced) ^2))
> full
Call:
lm(formula = lpsa ~ ., data = dat.tr)
Coefficients:
(Intercept) lcavol lweight age lbph svi lcp
0.629841 0.575148 0.568766 -0.024590 0.094223 0.691748 -0.128993
gleason pgg45
0.032534 0.005683
> reduced
Call:
lm(formula = lpsa ~ lcavol + svi + lcp, data = dat.tr)
Coefficients:
(Intercept) lcavol svi lcp
1.4460 0.6227 0.6470 -0.0394